Persamaan Garis Lurus

 ilustrasi:

Ilustasi:

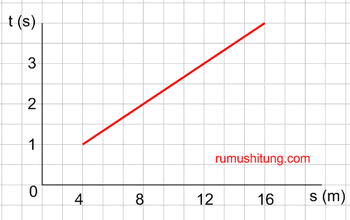
“Sobat CFD-an disekitar bundaran HI dengan menggunakan sepeda dan mengayuhnya dengan kecepatan tetap. Setiap selang 10 detik sobat menempuh jarak 40 m. Setiap detik seobat menempuh jarak 4 m. Berapakah jarak yang akan berhasil ditempuh selama 30 menit?”

Perhitungan untuk menyelesaikan soal tersebut jika dibuat tabel dan digambarkan dalam koordinat cartesius akan membentuk sebuah garis lurus. Garis ini terbentuk oleh sebuah persamaan yang disebut dengan persamaan garis lurus

Tabel Jarak terhadapWaktu

Waktu	Jarak Tempuh Sepeda
1	4
2	8
3	12
4	16
5	20
dan seterusnya

Tabel hubungan antara waktu dan jarak di atas jika diletakkan pada diagram cartesius akan membentuk sebuah garis lurus. Jadi fungsi atau persamaan yang menghubungkan antara waktu dengan jarak tempuh sobat merupakan suatu fungsi atau persamaan garis lurus.

“Jadi persamaan garis lurus adalah suatu persamaan yang apabila digambarkan ke dalam bidang koordinat cartesius akan membentuk sebuah garis lurus.”

Menggambar Persaman Garis Lurus pada Bidang Cartesius

Cara paling mudah menggambarkan persamaan garis lurus adalah dengan mencari nilai x dan nilai y secara acak. Biasanya menggunakan titik dengan nilai x = 0 dan nilai y = 0. Sobat hanya memerlukan dua titik untuk menggambarkan sebuah persamaan garis lurus. Berikut contohnya:

Gambarlah garis dari persamaan x + 2y = 10

Sobat buat dulu tabel pembantu dengan nilai x = 0 dan nilai y = 0 seperti berikut

Nilai x	Nilai y
0
	0

Kemudian lengkapi tabel di atas dengan memasukkan nilai x = 0 ( x + 2y = 10 → 0 + 2y = 10 → y = 5) dan untuk nilai y = 0 (x+2y = 10 → x + 2(0) = 10 → x = 10). Setelah dilengkapi tabelnya menjadi

Nilai x	Nilai y
0	5
10	0

Sekarang sobat telah mendapatkan dua buah titik yang bisa digunakan untuk menggambar garis dari persamaan tersebut.

 

Gradien

Pernahkah sobat mendaki sebuah gunung? Ketika mendakinya sobat akan menyusuri lereng. Lerang gunung ini memiliki kemiringan yang berbeda-beda. Analogi gradien sama seperti lereng gunung. Jika lereng adalah tingkat kemiringan gunung maka gradien adalah tingkat kemiringan sebuah garis lurus.

Bagaimana Menghitung Gradien?

Banyak cara untuk mencari besarnya gradien sebuah garis tergantung pada bentuk persamaan garis dan titik koordinat yang diketahui.

a. Mencari Gradien Persamaan Garis y = mx

Gradien bisa sobat cari dengan perbandingan antara ordinat dan absis. Rumusnya:

Gradien = Ordinat / Absis
m = y/x
y = mx

Sobat bisa mengatakan bahwa gradien adalah koefisien x jika persamaan garis dibuat dalam y = …

b. Mencari Gradien Persamaan Garis y = mx + c

Sobat tidak perlu bingung dengan bentuk persamaan yang berbeda yakni y = mx + c. Caranya sama. Sobat hanya perlu melihat koefisien x dalam persamaan y = mx + c.

Contoh
Tentukan gradiend dari persamaan garis
2y = x + 6
y = 1/2 x + 3
jadi gradiennya adalah 1/2

c. Mencari Gradien Persamaan Garis ax + by + c = 0

Tidak berbeda dengan cara sebelumnya, gradien dalam persamaan garis lurus berbentuk ax + by + c dapat dicari dengan terlebih dahulu mengubahnya ke bentuk y = mx + c. Koefisien dari variabel x (m) merupakan gradien dari garis tersebut.

Contoh
3x + 2y – 8 = 0
2y = -3x + 8
y = -3/2 x + 4
gradien = -3/2

d. Mencari Gradien Garis melalui dua titik

Untuk mencari gradien garis dari sebuah titik sama seperti membandingkan bergeraknya garis pada sumbu y dibagi bergeraknya garis pada sumbu x. Sobat bisa langsung menggunakan rumus

Contoh
Sebuah garis lurus melewati titik A(3,4) dan B (5,8). Tentukan gradien dari garis tersebut.

Jawab

Mengenal Sifat-sifat Gradien Garis Lurus

• Garis yang sejajar dengan sumbu x gradiennya adalah nol.
• Garis yang sejajar dengan sumbu y tidak memiliki gradien (tidak memiliki kemiringan).
• Gradien dua garis yang sejajar adalah sama, m1 = m2
• Hasil kali gradien dua buah garis yang saling tegak lurus adalah = -1

Rumus Menentukan Persamaan Garis

Diketahui	Rumus Persamaan Graris Lurus
Gradien (m) dan titik koordinat A (x1,y1)
Melalui duat titik (x1,y1) dan (x2,y2)

Menentukan Titik Potong Dua Buah Garis Lurus

Perhatikan gambar dua buah garis lurus di atas. Antara garis k dan garis l saling berpotongan pada seubah titik yaitu di titik A (x1,y1). Jika sobat diberikan data persamaan garis k dan l, dapatkah kalian menentukan dimana lokasi titik potong dari kedua garis lurus tersebut? Ada dua cara yang bisa sobat tempuh untuk menemukan koordinat titik A sebagai berikut:

a. Menggunakan Grafik

Cara ini sama sekali tidak recomended jika ini sobat pakai untuk menjawab soal ujian atau soal ulangan kecuali memang diminta dengan cara ini. Untuk menemukan titik potong sobat bisa menggambar kedua persamaan garis pada diagram cartesius untuk kemudian diamati secara langsung di mana lokasi titik potongnya.

b. Menggunakan Metode Substitiusi

Pada titik potong, nilai x1 dan y1 akan memenuhi kedua persamaan. Sobat bisa melakukan substitusi y pada persmaan yang satu ke y pada persamaan yang lain. Setelah itu nanti akan ketemu nilai x. Lebih jelasnya perhatikan contoh berikut:

Coba sobat tentukan koordinat titik potong antara garis 3x + y = 5 dan garis 2x – 3y = 7.

Untuk mencari titik potongnya ikuti langkah-langkah sebagai berikut:

1. sobat ambil salah satu persamaan, terserah. misal kita ambil 3x + y = 5
2. Kita ubah 3x + y = 5 → y = -3x + 5 dan kemudian kita substitusikan ke persamaan 2x – 3y = 7
3. 2x – 3y = 7
   2x – 3(-3x+5) = 7
   2x + 9x – 15 = 7
   11 x = 22
   x = 2
4. Setelah ketemu x kita masukkan ke salah satu persamaan untuk menentukan nilai dari y
   3x + y = 5
   3(2) + y = 5
   6 + y = 5
   y = 5-6 = 1
5. Jadi titik potong dari kedua garis lurus tersebut adalah di titik (2,1)

Soal Cerita Persamaan Garis Lurus

Beberapa tipe soal cerita matematika SMP bisa diselesaikan menggunakan persamaan garis lurus. Berikut contohnya.

Sobat membeli dua buah jeruk dan tiga buah manggis seharga Rp.800. Diketahui harga sebuah jeruk dan lima bua manggis adalah Rp.1.100. Tentukan berapa harga

a. sebuah jeruk
b. sebuah manggis
c. 4 buah jeruk dan 3 buah manggis

Soal tersebut di atas mirip dengan dua buah persamaan garis lurs. Untuk menyelesaikannya sobat bisa menggunakan permisalan bahwa harga 1 buah jeruk adalah x dan harga 1 bauah manggis adalah y kemudian kita buat kalimat matematikanya.

2x + 3y = 800 … (1)
x + 5y = 1100 … (2)

Kita ubah persamaan (2) dan menyubtitusikannya ke persamaan (1)

x + 5y = 1100
x = 1100 – 5y
2x + 3y = 800
2 (1100-5y) + 3y = 800
2200 – 10 y + 3y = 800
– 7 y = – 1400
y = 200
x = 1100 – 5y
x = 1100 – 5(200)
x = 1100 – 1000
x = 100

a dan b. Jadi harga satu buah jeruk adalah 100 dan harga satu buah manggis adalah 200.

c. Harga 4 buah jeruk dan 3 buah manggis = 4 (100) + 3(200) = 1000

Catatan : Penyelesaian soal persamaan garis lurus sebenarnya bisa juga menggunakan metode eliminasi.