Anggota himpunan dan diagram venn


Materi himpunan dan diagram venn memiliki keterkaitan yang erat. Himpunan menyatakan anggota yang tergabung dalam sebuah syarat tertentu. Sedangnkan diagram venn menggambarkan himpunan tersebut dalam sebuah diagram agar lebih mudah dipahami.
Contoh:
Himpunan bilangan Asli
Anggota: {1, 2, 3, 4, 5, 6, 7, …}
Himpunan bilangan prima kurang dari 13
Anggota:{2, 3, 5, 7, 11}

Hubungan himpunan dan diagram venn dapat dilihat pada gambar di bawah.
Himpunan
A = himpunan bilangan ganjil < 15 A = {1, 3, 5, 7, 9, 11, 13}   B = himpunan bilangan kelipatan tiga yang kurang dari 17 B = {3, 6, 9, 12, 15}

Diagram Venn
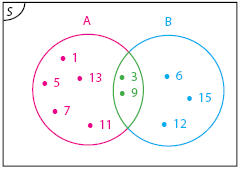
Himpunan dan Diagram Venn

Himpunan

Himpunan merupakan kumpulan benda atau objek yang didefinisikan dengan jelas. Lambang untuk menyimbolkan himpunan adalah huruf besar, misal A, B, C, dan lain sebagainya. Untuk menyatakan anggota dari sebuah himpunan adalah \in. Sedangkan untuk menyatakan anggota yang tidak termasuk dalam sebuah himpunan adalah \notin. Untuk menyatakan banyaknya anggota suatu himpunan A dinotasikan dengan n(A).
Contoh:
Himpunan A = {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Banyak anggota himpunan A = n(A) = 9
Himpunan memiliki anggota yang terhingga atau tak terhingga. Himpunan dengan banyak anggota terhingga atau dibatasi samoai batas tertentu disebut himpunan berhingga. Sedangkan, himpunan dengan banyak anggota tak terbatas adalah himpunan tak berhingga.
Contoh:
Himpunan berhingga: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
Himpunan tak berhingga: {25, 27, 29, 31, …}
Himpunan dapat dinyatakan dalam salah satu cara di bawah.
Menyebutkan semua anggotanya
Contoh: {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; {25, 27, 29, 31, …}; dan lain sebagainya.
Menuliskan sifat anggotanya
Contoh: himpunan bilangan asli kurang dari 10, himpunan bilangan ganjil lebih dari 23, dan lain sebagainya.
Notasi pembentuk himpunan
Contoh: {x | x < 10, x \in bilangan asli}, {x | x > 23, x \in bilangan ganjil}, dan lain sebagainya.

Macam-Macam Himpunan
Himpunan Semesta
Himpunan semesta adalah himpunan yang memuat semua anggota himpunan. Notasi untuk himpunan semesta adalah S.

Himpunan Bagian
A merupakan himpunan bagian B jika setiap anggota himpunan A merupakan anggota himpunan B. Notasi untuk menyatakan himpunan bagian adalah C. Simbol untuk menyatakan A himpunan bagian B adalah . Himpunan kosong merupakan himpunan bagian dari setiap himpunan. Setiap himpunan merupakan himpunan bagian dari himpunan itu sendiri.
Rumus mencari banyaknya himpunan bagian.
Himpunan = A
Banyak anggota himpunan A = n(A)
Banyaknya himpunan bagian A adalah 2^{n(A)}
Contoh:
B = {1, 2, 3}
n(B) = 3
Banyaknya himpunan bagian B adalah 2^{3} = 8 yaitu { }; {1}; {2}; {3}; {1, 2}; {1, 3}; {2, 3}; {1, 2, 3}.
Himpunan Kosong
Himpunan kosong adalah himpunan yang tidak mempunyai anggota. Himpunan kosong akan selalu menjadi himpunan bagian dari anggota himpunan bagian. Notasi himpunan kosong adalah { } atau .

Hubungan Antarhimpunan

Pembahasan selanjutnya dalam materi himpunan dan diagram venn adalah hubungan antarhimpunan. Hubungan antarhimpunan meliputi irisan, gabungan, komplemen himpunan, dan selisih himpunan. Lebih lanjut mengenai keempatnya dapat dilihat seperti pembahasan di bawah.
Irisan
Irisan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota A dan anggota B.
  \[A \cap B = \left \{ x \mid x \in A dan x \in B \right \} \]
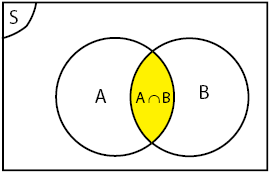
Irisan

Gabungan
Gabungan dua himpunan A dan B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A atau anggota himpunan B.
  \[ A \cup B = \left \{ x \mid x \in A atau x \in B \right \} \]
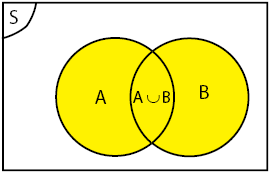
Gabungan

Komplemen
A^{C} adalah himpunan yang anggota-anggotanya merupakan anggota himpunan semesta namun bukan anggota himpunan A.
  \[A^{C} = \left \{ x \mid x \in S dan x \notin A\right \} \]
Komplemen

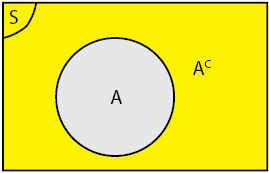
Selisih
A − B adalah himpunan yang anggota-anggotanya merupakan anggota himpunan A namun bukan anggota himpunan B.
  \[A - B = A \cap B^{C} \]
Selisih

Sifat-Sifat Operasi Himpunan

Pembahasan dalam materi himpunan dan diagram venn yang tidak kalah penting untuk dibahasa adalah sifa-sifat operasi pada himpunan. Sifat-sifat operasi himpunan meliputi komutatif, asosiatif, ditributif, dan dalil de Morgan.

Komutatif
  \[A \cap B = B \cap A \]
  \[A \cup B = B \cup A \]

Asosiatif
  \[\left(A \cap B \right) \cap C = A \cap \left( B \cap C \right) \]
  \[\left(A \cup B \right) \cup C = A \cup \left( B \cup C \right) \]

Distributif
  \[A \cap \left( B \cup C \right) = \left( A \cap B \right) \cup \left( A \cap C \right) \]
  \[A \cup \left( B \cap C \right) = \left( A \cup B \right) \cap \left( A \cup C \right) \]

Dalil de Morgan
  \[\left( A \cap B \right)^{C} = A^{C} \cup B^{C} \]
  \[\left( A \cup B \right)^{C} = A^{C} \cap B^{C} \]

Contoh Soal dan Pembahasan

Kelas VII-A terdiri dari 31 siswa. Terdapat 15 siswa mengikuti kompetisi Matematika, 13 siswa mengikuti kedua kompetisi IPA, dan 7 siswa tidak mengikuti kompetisi tersebut. Banyak siswa yang mengikuti kedua kompetisi tersebut adalah ….
A.       28 siswa
B.       8 siswa
C.       5 siswa
D.       4 siswa
SOAL UN Matematika SMP 2016
Pembahasan:
Misalkan: x = banyak siswa yang mengikuti kedua kompetisi.
Himpunan tersebut dapat digambarkan dalam bentuk diagram venn seperti gambar di bawah.
Contoh soal dan pembahasan matematika smp himpunan

Semua siswa = 31
  \[x + 15 - x + 13 - x + 7 = 31\]
  \[35 - x = 31\]
  \[x = 4\]
Jadi, banyak siswa yang mengikuti kedua kompetisi tersebut adalah 4 siswa.
Jawaban: D

Tidak ada komentar:

Posting Komentar

Langganan: Postingan (Atom)