MATEMATIKA: Persamaan linear dua variabel adalah sebuah persamaan yang memiliki dua jenis variabel berbeda dan berderajat satu.

Bentuk Umum: ax + by = c, dimana a,b,c E R Untuk mengetahui nilai setiap variabel, diperlukan paling sedikit dua persamaan. Dua persamaan tersebut dinamakan sistem persamaan linear dua variabel (SPLDV)
Sistem prsamaan dua linear dapat diselesaikan dengan 3 cara, yaitu substitusi, eliminasi, dan grafik.
a. Metode substitusi dilakukan dengan cara menyatakan salah satu variabel dengan variabel lainnya.
contoh:
Tentukan nilai x dan y yang memenuhi sistem persamaan x + 2y = 4 dan x - y = 1.
x + 2y = 4 -> x = 4 - 2y
Substitusikan x ke persamaan x - y = 1, diperoleh:
4 + 2y - y = 1
4 - 3y = 1
3 = 3y
y = 1
Substitusikan y = 1 ke persamaan x = 4 - 2y, diperoleh:
x = 4 - 2y
= 4 - 2 . 1
= 4 - 2
= 2
b. METODE ELIMINASI

Permasalahan dalam SPLDV:
Persamaan pertama: 2x + 3y = 8
Persamaan Kedua: 3x + y = 5

Penyelesaian permasalahan dengan metode eliminasi:
Langkah 1:

Langkah 2:
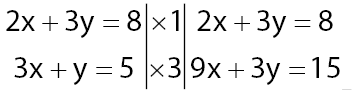
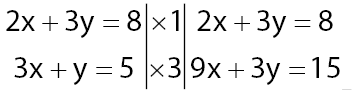
Metode Eliminasi SPLDV

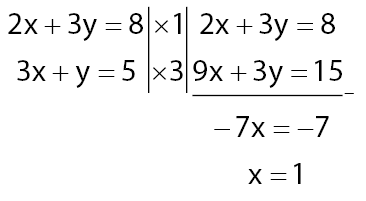
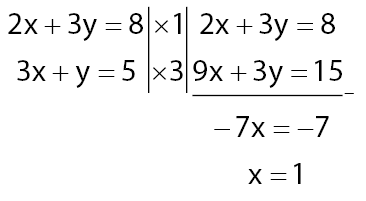
Langkah 3:
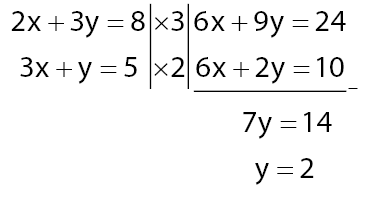
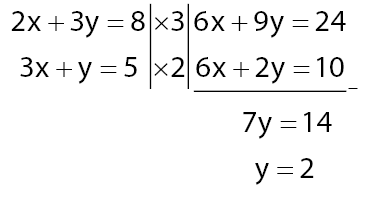
Metode Eliminasi SPLDV

Langkah 4:
Hasil yang diperoleh x = 1 dan y = 2
Penyelesaiannya adalah (1, 2)

Metode Gabungan (Eliminasi – Substitusi)
Metode gabungan merupakan penggabungan langkah dari metode sustitusi dan eliminasi. Metode eliminasi mempunyai langkah awal yang cukup mudah dan singkat. Sedangkan metode susbtitusi mempunyai cara akhir yang baik. Kedua metode tersebut digabungkan untuk mempermudah pengerjaan. Metode gabungan merupakan metode yang sering digunakan dalam menyelesaikan SPLDV.

Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:
  1. Cari nilai salah satu variabel x atau y dengan metode eliminasi.
  2. Gunakan metode substitusi untuk mendapatkan nilai variabel kedua yang belum diketahui.
  3. Penyelesaiannya adalah (x, y).

Permasalahan dalam SPLDV:
Persamaan pertama: 2x + 3y = 8
Persamaan Kedua: 3x + y = 5

Penyelesaian permasalahan SPLDV dengan metode gabungan (eliminasi – substitusi):
Langkah 1: mencari nilai x dengan metode eliminasi
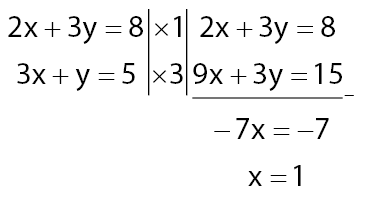
Sistem Persamaan Linear Dua Variabel (SPLDV))

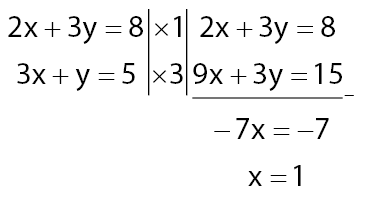
Sistem Persamaan Linear Dua Variabel (SPLDV))

Langkah 2: substitusi nilai $x=1$ pada persamaan 2x + 3y = 8 (pilih salah satu, bebas, hasilnya akan sama).

$2x + 3y = 8$

$2(1) + 3y = 8$

$2 + 3y = 8$

$3y = 8 - 2$

$3y = 6$

$y = \frac{6}{3} = 2$

Langkah 3: penyelesaiannya adalah (x, y)
Hasil yang diperoleh x = 1 dan y = 2
Penyelesaiannya adalah (1, 2)

Cara III: Metode Grafik
Penyelesaian SPLDV dengan metode grafik dilakukan dengan menentukan koordinat titik potong dari kedua garis yang mewakili kedua persamaan linear. Sebelumnya, sobat idSCHOOL perlu belajar mengenai cara menggambar garis pada persamaa linear terlebih dahulu.

Langkah-langkah menyelesaikan SPLDV dengan metode eliminasi:
  1. Menggbar garis yang mewakili kedua persamaan dalam bidang kartesius.
  2. Menemukan titik potong dari kedua grafik tersebut.
  3. Penyelesaiannya adalah (x, y).

Permasalahan dalam SPLDV:
Persamaan pertama: 2x + 3y = 8
Persamaan Kedua: 3x + y = 5

Penyelesaian SPLDV dengan metode grafik.
Langkah 1: menggambar kedua grafik
Menentukan titik potong pada kedua sumbu x dan y dari kedua persamaan.
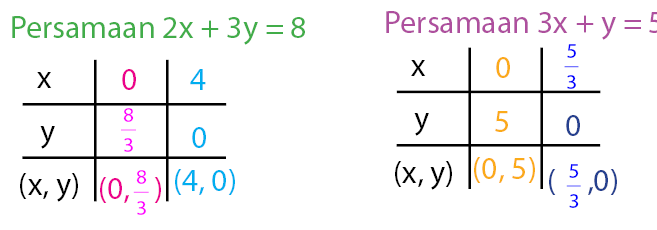
spldv

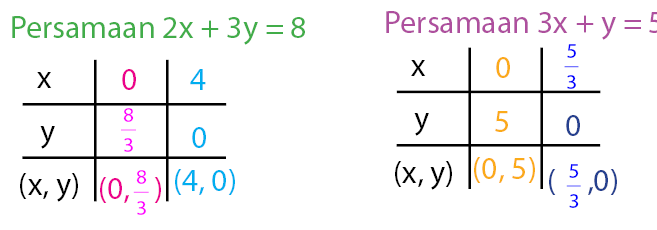
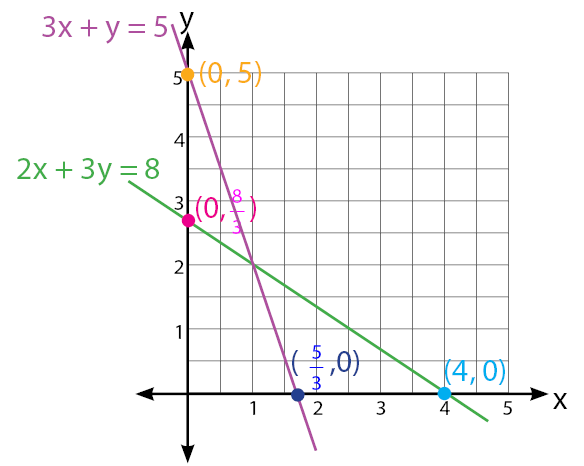
Reperesentasi kedua persamaan dalam bidang kartesius.

Langkah 2: menemukan titik potong dari kedua grafik tersebut.
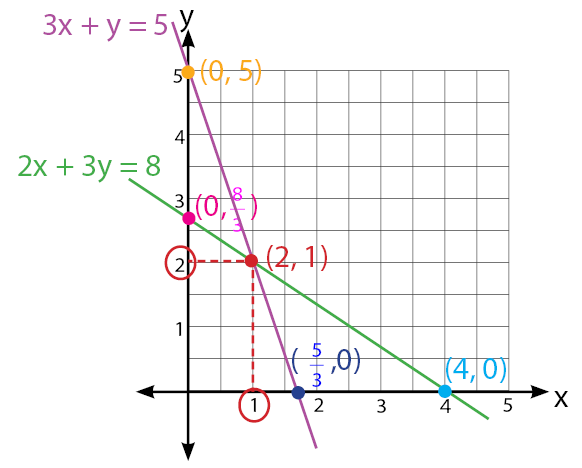
spldv metode grafik

Langkah 3: peyelesaiannya adalah (x, y)
Berdasarkan gambar dapat diketahui bahwa titik potong berada pada x = 1 dan y = 2
Penyelesaiannya adalah (1, 2)

Contoh Soal dan Pembahasan

Seorang tukang parkir mendapat uang sebesar Rp17.000,00 dari 3 buah mobil dan 5 buah motor, sedangkan dari 4 buah mobil dan 2 buah motor ia mendapat Rp18.000,00. Jika terdapat 20 mobil dan 30 motor, banyak uang parkir yang ia peroleh adalah ….
A. Rp135.000,00
B. Rp115.000,00
C. Rp110.000,00
D. Rp100.000,00

SOAL UN Matematika SMP 2016

Pembahasan:
Misalkan:
Tarif parkir per mobil = x
Tarif parkir per motor = y

Berdasarkan cerita pada soal, dapat diperoleh model matematika seperti di bawah.

$3x + 5y = 17.000$

$4x + 2y = 18.000$

Kalikan persamaan pertama dengan 4 (empat) dan persamaan kedua dengan 3 (tiga). Hal ini digunakan untuk membuat salah satu variabelnya sama, sehingga bisa saling mengurangi.
spldv metode eliminasi

Berdasarkan perhitungan di atas, diperoleh nilai y = 1.000
Subtitusi nilai y = 1.000 pada salah satu persamaan yang diketahui, misalnya 3x + 5y =17.000 (pemilihan persamaan yang berbeda akan tetap menghasilkan hasil akhir sama).

$3x + 5y = 17.000$

$3x + 5(1.000) = 17.000$